动物园

Time Limit: 10 Sec Memory Limit: 512 MB

Description

近日，园长发现动物园中好吃懒做的动物越来越多了。例如企鹅，只会卖萌向游客要吃的。为了整治动物园的不良风气，让动物们凭自己的真才实学向游客要吃的，园长决定开设算法班，让动物们学习算法。
　　某天，园长给动物们讲解KMP算法。
　　园长：“对于一个字符串S，它的长度为L。我们可以在O(L)的时间内，求出一个名为next的数组。有谁预习了next数组的含义吗？”
　　熊猫：“对于字符串S的前i个字符构成的子串，既是它的后缀又是它的前缀的字符串中（它本身除外），最长的长度记作next[i]。”
　　园长：“非常好！那你能举个例子吗？”
　　熊猫：“例S为abcababc，则next[5]=2。因为S的前5个字符为abcab，ab既是它的后缀又是它的前缀，并且找不到一个更长的字符串满足这个性质。同理，还可得出next[1] = next[2] = next[3] = 0，next[4] = next[6] = 1，next[7] = 2，next[8] = 3。”
　　园长表扬了认真预习的熊猫同学。随后，他详细讲解了如何在O(L)的时间内求出next数组。
　　下课前，园长提出了一个问题：“KMP算法只能求出next数组。我现在希望求出一个更强大num数组一一对于字符串S的前i个字符构成的子串，既是它的后缀同时又是它的前缀，并且该后缀与该前缀不重叠，将这种字符串的数量记作num[i]。例如S为aaaaa，则num[4] = 2。这是因为S的前4个字符为aaaa，其中a和aa都满足性质‘既是后缀又是前缀’，同时保证这个后缀与这个前缀不重叠。而aaa虽然满足性质‘既是后缀又是前缀’，但遗憾的是这个后缀与这个前缀重叠了，所以不能计算在内。同理，num[1] = 0,num[2] = num[3] = 1,num[5] = 2。”
　　最后，园长给出了奖励条件，第一个做对的同学奖励巧克力一盒。听了这句话，睡了一节课的企鹅立刻就醒过来了！但企鹅并不会做这道题，于是向参观动物园的你寻求帮助。你能否帮助企鹅写一个程序求出num数组呢？
　　特别地，为了避免大量的输出，你不需要输出num[i]分别是多少，你只需要输出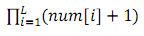img对1,000,000,007取模的结果即可。

img

Input

第1行仅包含一个正整数n ，表示测试数据的组数。随后n行，每行描述一组测试数据。每组测试数据仅含有一个字符串S，S的定义详见题目描述。数据保证S 中仅含小写字母。输入文件中不会包含多余的空行，行末不会存在多余的空格。

Output

包含 n 行，每行描述一组测试数据的答案，答案的顺序应与输入数据的顺序保持一致。对于每组测试数据，仅需要输出一个整数，表示这组测试数据的答案对 1,000,000,007 取模的结果。输出文件中不应包含多余的空行。

Sample Input

3
　aaaaa
　ab
　abcababc

Sample Output

36
　1
　32

HINT

n≤5 , L≤1,000,000

Main idea

定义一种前缀，这个前缀和后缀一样并且没有交集，num[i]为前i位有多少个这样的前缀，求题目中的式子。

Solution

看到这道题，我们一眼想到了从KMP的角度开始考虑。

然后我们想到了怎么暴力，显然就是把 fail[i]->i ，然后对于每个 i 的 num[i] ，一步步往上跳直到符合条件位置，那个位置的dep也就是num[i]。

我们想想这个过程优化吗？答案显然是可以的！我们运用倍增。

怎么倍增呢？直接从小到大枚举，可行就跳不一定最优。那么我们逆向思维，这么来想：一个点往上跳，跳到的最上面的不可行的位置的上一个显然就是最下面的可行的位置，那么我们可以从大到小枚举然后不合法的话往上跳，最后再跳一步即可。

由于这是带log的做法，我们要卡卡常，这里有一个小技巧：把数组最右边的那一维连续的话访问效率更高。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<bits/stdc++.h>
using namespace std;
typedef long long s64;

const int ONE=1000005;
const int MOD=1000000007;

int T;
int n;
char a[ONE];
int fail[ONE];
int LOG[ONE],f[21][ONE],Dep[ONE];
int Ans;

int get()
{
    int res=1,Q=1;char c;
    while( (c=getchar())<48 || c>57 )
        if(c=='-')Q=-1;
    res=c-48;
    while( (c=getchar())>=48 && c<=57 )
        res=res*10+c-48;
    return res*Q;
}

void Deal_KMP(char a[])
{
    int j=0;
    Dep[1]=1;
    for(int i=2;i<=n;i++)
    {
        while(a[j+1] != a[i] && j) j=fail[j];
        if(a[j+1] == a[i]) j++;
        fail[i] = j;
        f[0][i] = j;  Dep[i] = Dep[j]+1;
    }
}

void Dfs()
{
    for(int u=1;u<=n;u++)
        for(int i=0;i<=LOG[Dep[u]];i++)
            f[i+1][u] = f[i][f[i][u]];
}

int Deal_Ans(int x,int Limit)
{
    for(int i=LOG[Dep[x]];i>=0;i--)
        if(f[i][x] > Limit) x = f[i][x];
    return Dep[f[0][x]];
}

int main()
{
    T=get();
    for(int i=2;i<=ONE-1;i++) LOG[i]=LOG[i>>1]+1;
    while(T--)
    {
        scanf("%s",a+1);    n=strlen(a+1);
        Deal_KMP(a);        Dfs();

        Ans=1;
        for(int i=1;i<=n;i++)
        {
            Ans = (s64)Ans * ( Deal_Ans(i,i>>1)+1 ) % MOD;
        }

        printf("%d\n",Ans);
    }
}